Support Vector Machines

The Support Vector Machine (SVM) is another form of supervised learning of a binary classifier (see my post on the Perceptron). Specifically, SVM’s are a type of margin maximizers, that along with a kernel (more on this some other time), can become a very powerful tool.

Other models for supervised learning of a binary classifier, such the Rosenblatt Perceptron algorithm, can guarantee convergence, but there is no guarantee on “how good” the hyperplane it will find is. The key insight that led to the derivation of SVMs was the idea that we would not only like our model to converge, but would like our model to give us the “best possible” hyperplane. Although, how does one define the “best possible” hyperplane? Well, SVMs define this as the hyperplane that maximizes the distance between the two binary classes. We will define this distance as the margin. Therefore SVMs try to maximize this margin.

The Margin

Given a dataset $X \in \mathbb{R}^{D x N}$ with binary labels $y \in \{ -1, 1 \}$, weights $w \in \mathbb{R}^{D x 1}$, and a bias $b \in \mathbb{R}$, we define the margin $\mathcal{M}$ as the distance from the hyperplane $\mathcal{H}$ (given by $w^Tx+b=0$) to the closest point $x_{i} \in X$.

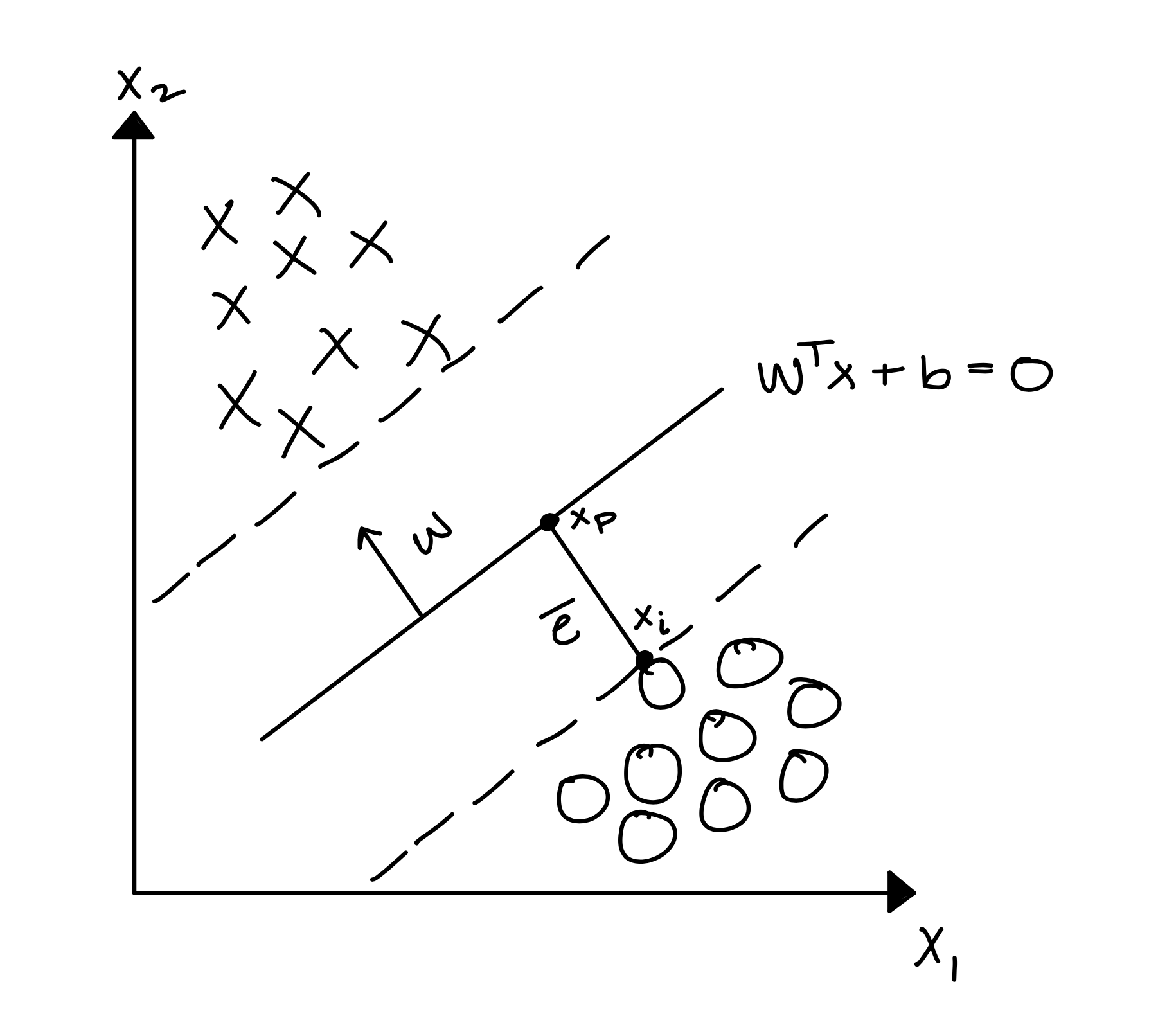
To formalize the definition of the margin $\mathcal{M}$ lets first formalize the distance from the hyperplane $\mathcal{H}$ to some point $x_{i}$. First, notice that if we project $x_{i}$ onto $\mathcal{H}$ we get another point denoted $x_{p}$ (see Figure 1) such that the distance from $x_{i}$ to the hyperplane is simply the distance between the two points. More formally, the distance from $\mathcal{H}$ to $x_{i}$ is $||\vec{e}||_{2}$ where $\vec{e} = x_{i} - x_{p}$.

Next, notice that because $\vec{e}$ represents the minimum distance between $x_{i}$ and $\mathcal{H}$ that it will also be orthogonal to $\mathcal{H}$ and parallel to $w$. Therefore we can rewrite $\vec{e}$ as $\vec{e} = \alpha w$, for some unknown $\alpha$. Additionally, since we know $x_{p}$ lies on the hyperplane, then it must be true that $w^T x_{p} + b = 0$. Using this fact, we can derive the following line of reasoning:

Now, we can use this definition of $\alpha$ to rewrite the length $||\vec{e}||_{2}$ as a function of $w$, $b$, and some $x_{i}$:

Then finally, the margin $\mathcal{M}$ given some hyperplane $\mathcal{H}$ and dataset $X$ is given by:

Primal Form Derivation:

SVMs are a type of “margin maximizers”. That is, we want to maximize the $M$. We can formalize this with the following optimization problem:

Notice one last thing, with this definition of the margin we could find some hyperplane that is infinitely far from out data that will satisfy this optimization problem. Therefore we must add an essential constraint that: $y_{i}(w^Tx_{i} + b) \geq 0 \;\;\; \forall x_{i} \in X$. Using this, we once again rewrite the optimization problem as:

The above optimization problem is rather ugly, the maximization of a minimization with an inequality constraint does not look fun to optimize. Preferably we would like to simplify this by removing the inner minimization. To do so, notice that $w$ is scale invariant. That is, $cw \; \forall c \in \mathbb{R}$ still defines the same hyperplane. Therefore, we can always find some $w$ such that $\min_{x_{i}} | w^Tx_{i} + b | = 1$. This constraint allows us to simplify the above objective as:

Then notice that if $\min_{x_{i}} | w^Tx_{i} + b | = 1$ then it must be true that $| w^Tx_{i} + b | \geq 1 \;\; \forall x_{i} \in X$, and we can simplify our constraint even further:

As Kilian Weinberger once said, “maximization is for losers.” So notice that the maximization of the reciprocal of $f(x)$ is just the minimization of $f(x)$. That is, we can rewrite our formulation as:

One last thing before we are done with the derivation of the SVM primal form. We cannot optimize $|| w ||_{2}$ as we need it to be twice differentiable where it’s currently linear. So we write out the final SVM primal form as:

This is the primal form of the SVM problem that we aim to optimize over.

The Lagrangian and the Karush-Kuhn-Tucker (KKT) Conditions

Consider the constrained optimization problem with inequality constraints in the form:

Such that $f(w)$ and $g_{i}(w)$ are convex, and $h_i(w)$ is affine. We call this form the primal optimization problem where the number of inequalities is $u$ and the number of equalities is $v$. Furthermore, we define the generalized Lagrangian of this form to be:

Such that $\alpha$ and $\beta$ are the Lagrange multipliers. We would like to know when the generalized Lagrangian is equal to the primal form. To do this first consider two quantities. The first quantity:

Given this quantity we can consider two cases: The first case is when $w$ takes on a value that satisfies the primal constraints. In this case we can see that $\mathcal{P}(w) = f(w)$. In the other case, the case that $w$ violates the primal constraints, we will have $\mathcal{P}(w) = \infty$. To formalize this we get:

Thus this form gives the same values of the primal form when $w$ satisfies the primal constraint. Therefore, we can write an equivalent statement to the primal form as the following:

Now lets consider the second quantity:

Then we define the dual of this form as follows:

Now lets compare these two quantities: Let $\hat{P}$ be the optimal value of $\min_{w} \mathcal{P}(w)$ and $\hat{D}$ be the optimal value of $max_{\alpha, \beta} \mathcal{D}(w)$. Then if follows that because $\min \max \geq \max \min$ that:

This inequality $\hat{P} \geq \hat{D}$ is called weak duality where the difference $\hat{P} - \hat{D}$ is called the duality gap. This inequality is always true even under non-convex conditions. Though we would like know under what conditions strong duality ($\hat{P} = \hat{D}$) holds, this happens exactly when the duality gap is 0. By Slater’s theorem (I will not be proving it here) we can show that strong duality holds in the case that:

1. $f(x)$ and $g_i(x)$ is convex. $h_j(x)$ is affine.
2. $\exists w$ such that $g_i(w) < 0$.

For the hard margin SVM, there is no equality constraint $h_j(x)$. We know that $f(x)$ is convex and $g_i(x)$ is affine and therefore convex. Therefore, Slater’s conditions hold under the assumption that $\exists w$ such that $g_i(w) < 0$, which is true if there exists some hyperplane that separates our data (as we will let $g_i(w) = -y_i(w^Tx_i + b) + 1 \leq 0$).

Under these conditions we will have some optimal values $\hat{w}$, $\hat{\alpha}$, and $\hat{\beta}$ that additionally satisfy the Karush-Kuhn-Tucker (KKT) conditions, which are as follows:

1. $\frac{\partial}{\partial w_{i}} \mathcal{L}(w, \alpha, \beta) = 0 \; \forall i = 1, 2, ..., n$
2. $\frac{\partial}{\partial \beta_{i}} \mathcal{L}(w, \alpha, \beta) = 0 \; \forall i = 1, 2, ..., v$
3. $\alpha_{i}(g_{i}(w)) = 0 \; \forall i = 1, 2, ..., u$
4. $g_{i}(w) \leq 0 \; \forall i = 1, 2, ..., u$
5. $\alpha_i \geq 0 \; \forall i = 1, 2, ..., u$

Dual Form Derivation:

The SVM primal form is a constrained optimization problem and can be solved using Lagrangian multipliers. Taking into account the above notes we let $g_i(w) = -[y_i(w^Tx_i + b) - 1] \leq 0$. Notice we do not have any equality constraints, then the Lagrangian of the SVM primal form is the following:

Considering the KKT condition #1, we take the partial derivatives w.r.t. $w$ and $b$ which gives:

Looking back at our original Lagrangian equation and plugging $w = \sum_{i = 1}^{n} \alpha_{i} y_{i} x_{i}$ and $\sum_{i = 1}^{n}\alpha_{i} y_{i} = 0$ in allows us to simplify:

Which leaves us with the final SVM Dual Form and the following optimization problem:

This SVM Dual Form will be the main focus of the practical implementation of this algorithm as we can optimize this form using quadratic programming and convex optimization libraries in Python such as CVXOPT .

Deriving the Weights and Bias from the Dual Form

We already have a known solution for the weights that satisfies the KKT condition #1. That being: $w = \sum_{i = 1}^{n} \alpha_{i} y_{i} x_{i}$. Taking into account the KKT condition #3, notice that $\alpha_{i}(y_{i}(w^Tx_{i} + b) - 1) = 0$ where $\alpha_i \geq 0$. This leaves us with two main conditions, either $\alpha_{i}$ is 0 and we are not dealing with a support vector, or $y_{i}(w^Tx_{i} + b) = 1$ in which case we are dealing with a support vector. We can ignore the case in which $\alpha_{i} = 0$ and deal solely with the case regarding the support vector. Simplifying the support vector case gives the following:

The equation above gives the bias for some support vector where $\alpha_{i} \geq 0$. To find the bias of the hyperplane, we can just take the mean average over each support vector bias. Resulting in:

In most cases this will just equal the average over all support vector biases, though this will not always be true. In fact, I have seen multiple sources say that this is true and that the bias is equal to the mean over all support vectors biases, including myself at one point. Though I realized that if you have two points on one of your support vectors then taking the mean over all biases would skew your bias towards that support vector. So, you must be careful to only take the mean average over two bias terms (one on each support vector).

Python Implementation and CVXOPT

CVXOPT is a python library for convex optimization. It uses quadratic programming to solve the convex optimization problem of the following form:

We will use CVXOPT to build a Python implementation of the SVM. Much of the following code and design is modified from Aladdin Persson’s implementation (found here). His implementation of the SVM with CVXOPT was instrumental in my understanding, so a huge shout-out to him. Below I will show the core pieces of the code. The full code can be found on my GitHub.

import matplotlib.pyplot as plt
import numpy as np
import cvxopt

from mlxtend.plotting import plot_decision_regions
from sklearn.datasets import make_circles, make_blobs
from sklearn.svm import SVC

We’re going to implement the SVM class in the traditional scikit-learn fashion taking the following abstract form:

class SVM:
    def __init__(self):
        self.X = None
        self.y = None

    def fit(self, X, y):
        ...

    def transform(self, X, y):
        ...

To do this, let’s first implement the fit function. Though one problem does arise, we need to convert our dual form problem into something recognizable by CVXOPT. That is, we need to find a way to represent $P, q, G, h, A, b$. To do this I followed this article, although I have also posted my hand-written notes on this conversion here. If we let $x=\alpha$, then after some tedious algebra we can represent $P$, $q$, $G$, $h$, $A$, and $b$ as the following:

Where $I_{m}$ is an identity matrix of size $m \; x \; m$, and where the size of $X$ is $(m, n)$. In other words $m$ is how many samples of data we have. Given this, our fit function becomes the following:

class SVM:
    ...

    def fit(self, x: np.ndarray, y: np.ndarray) -> None:
        m, n = x.shape

        # Requires this shape and data type.
        y = y.copy().reshape(-1, 1).astype(np.float64)

        self.X = x
        self.y = y

        # Compute the inner product.
        self.kernel = np.dot(self.X, self.X.T)

        # See my notes above for how this was derived.
        P = cvxopt.matrix(np.outer(y, y) * self.kernel)
        q = cvxopt.matrix(-np.ones((m, 1)))
        G = cvxopt.matrix(np.vstack((-np.identity(m), np.identity(m))))
        h = cvxopt.matrix(np.vstack((np.zeros((m, 1)), np.ones((m, 1)))))
        A = cvxopt.matrix(y, (1, m), 'd')
        b = cvxopt.matrix(np.array([0]), (1, 1), 'd')

        optimal = cvxopt.solvers.qp(P, q, G, h, A, b)
        cvxopt.solvers.options["show_progress"] = True

        self.alphas = np.array(optimal['x'])

Next, we need to write the predict function. For SVMs, this will follow very closely with the above section on deriving the weights and bias from the dual form, and then using them to make the prediction.

class SVM:
    ...

    def predict(self, X: np.ndarray) -> np.ndarray:
        non_zero_alphas = (self.alphas > 1e-4).flatten()

        support_k = self.kernel[non_zero_alphas, non_zero_alphas][:, np.newaxis]
        support_x = self.X[non_zero_alphas]
        support_a = self.alphas[non_zero_alphas]
        support_y = self.y[non_zero_alphas]

        idx_0 = np.where(support_y == -1)[0][0]
        idx_1 = np.where(support_y == 1)[0][0]

        bias_0 = support_a[idx_0] * support_y[idx_0] * support_k[idx_0]
        bias_1 = support_a[idx_1] * support_y[idx_1] * support_k[idx_1]

        bias = -(bias_0 + bias_1) / 2

        predictions = support_a * support_y * np.dot(support_x, X.T)
        predictions = predictions.sum(axis = 0) + bias

        return np.sign(predictions)

The full code, and it’s implementation can again be found on my GitHub. Now let’s test out the performance of our model on some fake data. We’ll also compare it against the scikit-learn implementation of the SVM.

# Get the toy dataset.
X, y = make_blobs(n_samples = 200, centers = 2, random_state = 1)

y[y == 0] = -1
y_int_32 = y
y = y.reshape(-1, 1) * 1.0

# Our model.
model = SVM()
model.fit(X, y)

# sklearn implimentation for reference.
sklearn_model = SVC(kernel = "linear")
sklearn_model.fit(X, y_int_32)

# Visualize performance.
fig, (ax0, ax1) = plt.subplots(1, 2, figsize = (8, 3))

plot_decision_regions(X, y_int_32, clf = model,         legend = 2, ax = ax0)
plot_decision_regions(X, y_int_32, clf = sklearn_model, legend = 2, ax = ax1)

ax0.set_title("Custom")
ax1.set_title("scikit-learn")

plt.show()

Which gives:

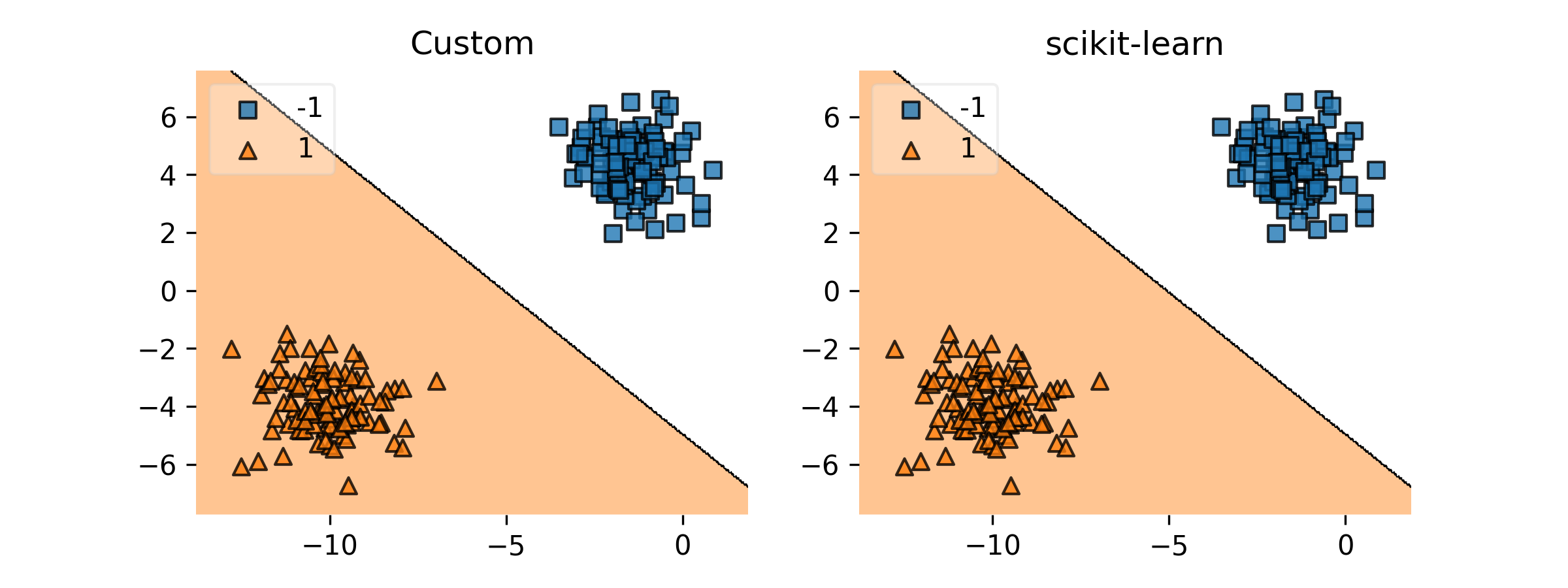
We can see that our model gives a nice separation of the data, and performs the same as the scikit-learn implementation.

Conclusion

In this post, we introduced the Support Vector Machine (SVM), a model for supervised learning of a binary classifier. We explored the mathematical foundations of SVMs, starting from the concept of margin maximization, and then derived both the primal and dual optimization forms. We also introduced and discussed the Karush-Kuhn-Tucker (KKT) conditions, and their role in solving the SVM optimization problem. Finally, we showed a practical implementation of an SVM in Python, using the CVXOPT library, and compared our implementation with scikit-learn’s.

References

1. Cortes, C., Vapnik, V.N. (1995). Support-Vector Networks. Link
2. Vapnik, V.N. (1997). The Support Vector method. Link
3. M. S. Andersen, J. Dahl, and L. Vandenberghe. (2012). CVXOPT: A Python package for convex optimization. Link
4. Persson, A. (2020). SVM from Scratch - Machine Learning Python (Support Vector Machine). Link
5. Xavier, S. B. (2018). Support Vector Machine: Python implementation using CVXOPT. Link
6. Andrew, NG (). CS229 Lecture notes. Link
7. Weinberger, K. (2018). Lecture 9: SVM. Link
8. Gordon, G., Tibshirani, R. (). Karush-Kuhn-Tucker conditions. Link

Figures

1. Custom image.
2. Example of the SVM and scikit-learn fit on a dataset. Link.